Из журнала Scenergy #2, Новгород, 2000
;-----------------------------------------
;-TEXTURE MAPPING- ESPECIALLY 4 SCENERGY
;-----------------------------------------
(C) 1999 SaiR00S/EI
Суть линейного текстурного мэппинга
заключается в линейной интерполяции
координат полигона и соответствующим им
текстурных координат.
В качестве полигона чаще всего
выбирается треугольник, хотя описанный
ниже алгоритм подходит для любого
полигона.
Итак, полигоном является треугольник,
все вершины которого имеют пары координат
(X,Y) и связанные с ними текстурные
координаты (U,V). По полигону мы будем
двигаться сверху-вниз и слева-направо ,
т.е при движении сверху-вниз мы будем
увеличивать на каждом вертикальном шаге
координату Y треугольника при
одновременной линейной интерполяции
координаты X и текстурных координат (в
итоге получится контур полигона и
соответствующий ему контур треугольника в
текстуре), а при движении слева-направо,
увеличивая координату X-координату от
левой границы контура до правой на
единицу, проводим линейную интерполяцию по
текстуре и ставим в координату Xi,Yj
значение цвета из текстуры по координатам
Up,Vq.
Первое , что необходимо сделать - это
отсортировать координаты треугольника
вmeсте с текстурными координатами в
порядке возрастания координаты Y, т.е.
If vert1.y > vert2.y then
swap (vert1,vert2);
If vert2.y > vert3.y then
swap (vert2,vert3);
If vert3.y > vert1.y then
swap (vert3,vert1);
Или (лексика STORM'a):
LD HL,(VERT1); Берем X,Y координа-
LD DE,(VERT2); ты треугольника
LD BC,(VERT3);
EXX
LD HL,(VERT1+2); Берем текстурные
LD DE,(VERT2+2); координаты U,V
LD BC,(VERT3+2);
EXX
LD A,D
CP H
JR NC,NOSWAP1
EX DE,HL
EXX
EX DE,HL
EXX
NOSWAP1 LD A,B
CP H
JR NC,NOSWAP2
LD A,L,L,C,C,A
LD A,H,H,B,B,A
EXX
LD A,L,L,C,C,A
LD A,H,H,B,B,A
EXX
NOSWAP2 LD A,B
CP D
JR NC,NOSWAP3
LD A,E,E,C,C,A
LD A,D,D,B,B,A
EXX
LD A,E,E,C,C,A
LD A,D,D,B,B,A
EXX
NOSWAP3 LD (VERT1),HL
LD (VERT2),DE
LD (VERT3),BC
EXX
LD (VERT1+2),HL
LD (VERT2+2),DE
LD (VERT3+2),BC
EXX
В результате получается картина,
изображенная на рисунке. В данном случае
точка перегиба находится слева,
соответственно, в левой половине
треугольника имеем 2 грани, а в правой -
одну.
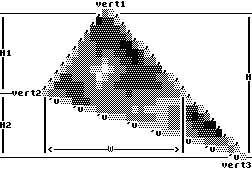
Ha рисунке:
H - максимальная высота треугольника
H1 - высота ребра (vert1,vert2);
H2 - высота ребра (vert2,vert3);
W - наибольшая ширина треугольника
треугольника по X. Определяется
она следующим образом:
t=(vert2.y-vert1.y)/(vert3.y-vert1.y)
w=(vert1.x+t*(vert3.x-vert1.x))-vert2.x
Если H и/или W равны нулю, то
треугольник рисовать не нужно.
Далее определяется с какой стороны
находится точка перегиба в треугольнике.
Делается это проверкой знака величины W.
Если эта величина положительна, то точка
перегиба - слева, отрицательна - справа.
If w>0 then "point" on left
else "point" on right
Затем проводим линейную интерполяцию
координаты X треугольника и текстурных
координат U,V. Интерполяцию можно
проводить по нижеприведенным формулам или
по Брезенхему - кому как нравится,но
второй вариант быстрее (хотя, при малом
количестве полигонов, что мы имеем на
Спектруме, это практически не заметно).
Итак, если точка перегиба слева (W>0),
то нужно отрисовать две грани слева и одну
справа:
Строим левую сторону треугольника:
h1=vert2.y-vert1.y
DeltaLeftX1=(vert2.x-vert1.x)/h1
DeltaLeftU1=(vert2.u-vert1.u)/h1
DeltaLeftV1=(vert2.v-vert1.v)/h1
h2=vert3.y-vert2.y
DeltaLeftX2=(vert3.x-vert2.x)/h2
DeltaLeftU2=(vert3.u-vert2.u)/h2
DeltaLeftV2=(vert3.v-vert2.v)/h2
X:=vert1.x;
For i=0 to h1 do
Begin
TableLeftX[i]:=X;
TableU[i]:=U;
TableV[i]:=V;
X:=X+DeltaLeftX;
U:=U+DeltaLeftU;
V:=V+DeltaLeftV;
End;
For i=h1 to h2 do
Begin
TableLeftX[i]:=X;
TableU[i]:=U;
TableV[i]:=V;
X:=X+DeltaLeftX2;
U:=U+DeltaLeftU2;
V:=V+DeltaLeftV2;
End;
Строим правую сторону треугольника:
h=vert3.y-vert1.y;
DeltaRightX=(vert3.x-vert1.x)/h;
For i=0 to h do
Begin
TableRightX[i]:=X;
X:=X+DeltaRightX;
End;
Здесь:
TableLeftX[] - таблица, содержащая X
координаты левой поло-
вины треугольника;
TableRightX[]- то же для правой поло-
вины;
ТableU[] - таблица, содержащая U
координаты левой поло-
вины треугльника;
TableV[] - то же для V-координаты
DeltaLeftX - константа интерполяции
(на ZX должна считать-
ся с fixed point 8.8);
DeltaRightX - то же.
Если же точка перегиба находится справа
(W<0), то все аналогично, только слева
отрисовываем одно ребро треугольника , а
справа - два.
Далее определяем шаги по текстуре ,
которые являются постоянными для всего
полигона (на ZX будем считать их с fixed
point 8.8, причем со знаком!):
DeltaU=(t*(u3-u1)+(u1-u2))/w
DeltaV=(t*(v3-v1)+(v1-v2))/w
Далее непосредственно рисуем полигон:
i:=0;
For Y:=vert1.y to (vert1.y+H) do
Begin
U:=TableU[i];
V:=TableV[i];
For X:=TableLeftX[i] to TableRigtX[i] do
Begin
{ставим точку в координату (X,Y) цвета
из текстуры по координате (U,V)}
PutPixel(X,Y,Texture[U,V])
X:=X+1;
U:=U+DeltaU;
V:=V+DeltaV
End;
i:=i+1
End;
Внутренний цикл будет выглядеть
следующим образом (кстати, возможно
быстрее...):
LD A,H; V-координата в текстуре
ADD HL,DE; вычисляем следующую ко-
; ординату V
EXX
LD B,A
LD C,H ; U-координата в текстуре
ADD HL,DE; вычисляем следующую ко-
; ординату U
LD A,(BC); берем тексель
EXX
LD (BC),A; помещаем тексель в бу-
; фер
INC C ; увеличиваем X-координа-
; ту
Следует напомнить, что все (почти)
вычисления проводятся с fixed point 8.8,
например:
HL=H.L, т.е H содержит целую часть
числа, а L - дробную.
Ну вот, вроде и все, удачи в кодинге.
