Из журнала Scenergy #1, Новгород, 1999
(C) Flying/DR
Реализация Phong Bump Mapping на Speccy.
0. Вступление
Материал, изложенный в этой статье на
данный момент, к сожалению уже утратил ту
актуальность, которую он имел на момент
своего написания (осень 1997-го :) ).
Однако, возможно, это до сих пор кому-то
интересно... Тем более что перед
публикацией я основательно поработал над
разделом касающимся оптимизаций.
Наблюдая в течении нескольких последних
лет за развитием спектрумовской сцены, я
прихожу к выводу, что процесс развития
искусства demomaking'а на Speccy идет
практически теми же темпами, что и на
"больших" платформах (Amiga,PC), при том,
что "железо" на котором все это работает
не претерпевает никаких изменений: все те
же 128кб и 3.5 MHz. А уровень эффектов в
demo постоянно растет, появляются новые
методы программирования, работы с экраном,
звуком и диском... А в результате
появляются эффекты аналогичные (почти)
тем, что реализуются на Amiga и PC. За
примерами далеко ходить не надо -
достаточно посмотреть на демы, занимавшие
первые места на ENLiGHT'97 и Funtop'98. И
это здорово!
Многие начинающие кодеры приходят в
восхищение от просмотра очередной
супернавороченной демы от какой-нибудь
известной команды и загораются желанием
реализовать нечто подобное. Но здесь
возникает проблема - большинство
современных эффектов - высший пилотаж
искусства программирования и ковыряться в
их коде, как правило, затруднительно,
а описания алгоритмов их работы найти
достаточно трудно. Поэтому данный раздел
журнала призван, хотя бы отчасти, помочь
получить так необходимые вам сведения об
алгоритмах работы эффектов в современных
demo.
И в этом номере в качестве "затравки" я
приведу алгоритм работы эффекта известного
как Phong Bump Mapping. Этот эффект
впервые появился где-то году в 1995 на
Amiga и PC и сразу приобрел широкую
популярность из-за своей простоты и
эффектности. На Speccy (насколько мне
известно) впервые был реализован в 1997
году в демах представленных на ENLiGHT'97:
Binary Love, Shit 4 Brainz (алгоритмически
там правда совсем не bump mapping, но
выглядит похоже), Power UP (только в final
release).
В качестве иллюстрации того, как выглядит
этот эффект (дабы вы имели представление,
о чем собственно идет речь) - приведу
экран из нашей demo Binary Love.

Визуально эффект представляет собой пятно
света, двигающееся по определенной траек-
тории и освещающее некое изображение,
причем это изображение рельефно, т.е. как
бы "выдавлено" на экране.
Итак, приступим...
1.Алгоритм работы
Как ни странно, но все гениальное просто.
Так и здесь - при всей своей эффектности
алгоритм здесь очень простой. Но для
начала немного математики для лучшего
понимания сути (кому математика стоит
поперек горла - может не читать).
Да, сразу скажу, что я далеко не спец в
математике и вполне могу ошибаться в
точности определений. Заранее прошу за это
прощения у профи.
1.1 Математическая модель
Сперва введем понятие нормали к
поверхности (если вы уже знаете, что
такое нормаль - пропустите этот абзац).
Для остальных поясню, что нормалью к
поверхности в данной точке называется
вектор с началом в данной точке и
направленный перпендикулярно плоскости.
Если же вы не знаете, что такое вектор,
то попробуйте посмотреть учебник по гео-
метрии :) Для лучшего понимания того, что
такое нормаль посмотрите на рис.1.
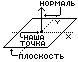
Теперь представим себе некую неровную
поверхность "в разрезе".
Для каждой точки данной поверхности можно
построить нормаль (см.рис.2).
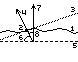
1 - поверхность.
2 - точка, в которой строим
нормаль.
3 - касательная в данной
точке.
4 - нормаль в данной точке.
5 - плоскость, на которую "насыпаны" все
неровности поверхности.
6 - угол между плоскостью (5) и нормалью
(4).
7 - нормаль к плоскости (5).
8 - угол между нормалями (4) и (7).
Из всего этого нам важен именно угол (8),
так как в нашем случае он характеризует
"степень освещенности" данной точки
источником света, расположенным прямо над
поверхностью. Т.е. чем меньше этот угол,
тем больше освещенность данной точки.
Естественно, что для случая 2-мерной
плоскости нам необходимо знать 2 таких
угла - по X и по Y, с тем, чтобы
определиться с ориентацией нормали.
Ну вот, с этим вроде бы разобрались.
Сразу хочу заметить, что все изложенное
выше не претендует на абсолютную
правильность с точки зрения физики и
математики, однако довольно точно поясняет
суть проблемы с точки зрения реализации
эффекта.
2. То же самое с точки зрения компьютера
Здесь все намного проще и понятнее. У нас
есть некая картинка, по которой мы хотим
заставить двигаться пятно света. Сразу
хочу заметить, что здесь картинка
задается не цветами, а как бы степенями
выпуклости точек, (высотами) т.е. точка с
"цветом" 7 при работе эффекта будет
казаться более "выпуклой" чем, например
точка с "цветом" 3. Хотя для Speccy вполне
подойдет и 2-хцветная картинка,
нарисованная, например в Art Studio.
Правда, нам необходима картинка с
разрешением 1 байт на точку (как если бы
мы рисовали ее атрибутами). Но проблемы
такой конвертации уже не относятся к делу.
Мы исходим из того, что у нас эта картинка
есть.
Тогда яркость каждой точки выходного
изображения считается следующим образом:
x,y - координаты точки, для которой
ведется расчет.
lx,ly - координаты "источника света"
Сначала находим вектор, построенный от
нашей точки к точке источника света
(назовем его L):
vlx=x-lx ;X координата вектора
vly=y-ly ;Y координата вектора
Теперь нам надо найти нормаль в данной
точке. Вообще-то если бы мы находили
нормаль по всем правилам математики, то
это было бы довольно сложно. Однако в
данном случае нам необходимо знать только
то, как эта нормаль направлена, т.е. знать
знаки ее X и Y составляющих. А это
делается очень просто - путем нахождения
разности между значениями "высоты" в
соседних точках соответственно по X и по
Y. Так мы получим псевдовектор нормали в
данной точке (назовем его N):
nx=Image(x+1,y)-Image(x-1,y)
ny=Image(x,y+1)-Image(x,y-1)
nx,ny - составляющие вектора N по X и Y.
Image - наша картинка (представленная в
виде двумерного массива).
Остальное достаточно просто. Нам надо
получить информацию о степени освещенности
нашей точки по осям X и Y:
Для X:
;Находим значение освещенности
col=abs(vlx-nx)
;Ограничиваем количество градаций яркости
if col>16 then col=16
;difx - степень освещенности нашей точки
;по X.
difx=16-col
;Убираем возможное "отрицательное
;освещение" :)
if difx<0 then difx=1
Для Y все то же самое:
col=abs(vly-ny)
if col>16 then col=16
dify=16-col
if dify<0 then dify=1
Ну вот, теперь мы имеем две составляющие
освещенности нашей точки по X и Y (difx и
dify соответственно). Общая освещенность
получается путем их усреднения:
col=(difx+dify)/2
Теперь осталось только поставить точку
соответствующего цвета - и все OK!
;Ограничиваем максимальную степень
;освещенности
if col>15 then col=15
;Убираем возможное "отрицательное
;освещение" и ставим точку
if col>0 then plot x,y
Как видите - ничего сложного здесь нет -
все просто и понятно. Однако здесь есть
одно "НО" - дело в том, что написав свой
эффект по приведенному выше алгоритму и
запустив вы, к сожалению, увидите не
совсем то, на что рассчитывали - пятно
света вместо красивого такого кружка будет
представлять собой ромб.
А дело тут в том, что аппроксимация
расстояния то точки велась линейно, а не
по формуле нахождения расстояния между 2-я
точками:
R=sqrt(sqr(x)+sqr(y))
Для того же, чтобы получить в качестве
пятна света круг - придется использовать
несколько другой алгоритм:
;Сначала все то же самое...
vlx=x-lx
vly=y-ly
nx=Image(x+1,y)-Image(x-1,y)
ny=Image(x,y+1)-Image(x,y-1)
;А теперь все несколько иное...
difx=abs(vlx-nx)
dify=abs(vly-ny)
col=15-sqrt(sqr(difx)+sqr(dify))
if col>15 then col=0
plot x,y
Надеюсь понятно? Все практически то же
самое, только расчет интенсивности
освещения ведется по формуле расстояния
между двумя точками, приведенной выше.
3. Особенности реализации на Speccy
Надеюсь, что любой кодер на Speccy,
взглянув на приведенный выше алгоритм
сразу поймет, что реализовать его "в лоб"
не удастся по причине необходимости
вычисления функций SQR и SQRT. И даже
представление этих функций в виде таблицы
не даст приемлемого по скорости
результата. Однако, взглянув еще более
внимательно можно заметить то, что и
позволит нам реализовать Phong Bump
Mapping на Speccy. Дело в том, что при
ограничении количества градаций яркости до
16 (чего вполне достаточно) мы получаем,
что все множество значений функции расчета
освещенности:
col=15-sqrt(sqr(difx)+sqr(dify))
спокойно укладывается в табличку размером
16*16=256 байт! Т.е. имея такую табличку,
мы сможем получать значение освещенности
всего за 3-4 команды ассемблера, просто
доставая число из таблицы!
И еще одна возможная оптимизация. Если
предполагается использовать Bump Mapping
для статического изображения, то можно
преобразовать это изображение в таблицу, в
которой для каждого пикселя исходного
изображения хранятся значения nx и ny. Это
еще более ускорит процесс построения
изображения (в качестве примера см.
исходный текст в приложении).
Все остальное, естественно рассчитывается
без особых усилий и в целом скорость
работы будет вполне приемлемая.
4. Дальнейшие оптимизации
Давайте посмотрим, что еще можно
соптимизировать... Для этого внимательно
посмотрите на dump рассчитанной таблицы
квадратного корня, а также на ее
визуальное представление:
F E D C B A 9 8 7 6 5 4 3 2 1 0
E E D C B A 9 8 7 6 5 4 3 2 1 0
D D C B B A 9 8 7 6 5 4 3 2 1 0
C C B B A 9 8 7 6 6 5 4 3 2 1 0
B B B A 9 9 8 7 6 5 4 3 2 1 0 0
A A A 9 9 8 7 6 6 5 4 3 2 1 0 0
9 9 9 8 8 7 7 6 5 4 3 2 2 1 0 0
8 8 8 7 7 6 6 5 4 4 3 2 1 0 0 0
7 7 7 6 6 6 5 4 4 3 2 1 1 0 0 0
6 6 6 6 5 5 4 4 3 2 2 1 0 0 0 0
5 5 5 5 4 4 3 3 2 2 1 0 0 0 0 0
4 4 4 4 3 3 2 2 1 1 0 0 0 0 0 0
3 3 3 3 2 2 2 1 1 0 0 0 0 0 0 0
2 2 2 2 1 1 1 0 0 0 0 0 0 0 0 0
1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

Интересно, правда? :) Оказывается, именно
эта таблица формирует внешний вид нашего
пятна света.
AAтDО Что нам это дает?
Во-первых, если мы имеем таблицу,
формирующую 1/4 пятна света, то ничто нам
не помешает сделать полное изображение
этого пятна. Допустим, мы это сделали. Что
мы теперь имеем?
1) Изображение, по которому мы собираемся
пустить источник света. Как уже было
сказано выше - каждая его точка должна
быть представлена в виде пары значений
(nx,ny).
2) Таблицу (а по сути - тоже изображение)
пятна света которое будет освещать наше
изображение.
Теперь давайте еще раз внимательно
проанализируем алгоритм работы эффекта
описанный выше:
vlx=x-lx
vly=y-ly
Подумайте, а как будут изменяться эти
значения? Вспомним, что для каждого кадра
lx и ly - константы! А x и y будут
изменяться в 2-х вложенных циклах:
for y=0 to Image_YSize-1
for x=0 to Image_XSize-1
;Рассчет освещенности в точке (x,y)
end x
end y
Т.е. получается, что если в начале
построения каждого кадра мы вычислим vlx и
vly, то потом их можно будет просто
интерполировать линейно, через обычный
INC.
А если посмотреть еще немного, то видно,
что в начале кадра x=0 и y=0, т.е. мы
имеем vlx=lx и vly=ly!
Идем дальше...
nx=Image(x+1,y)-Image(x-1,y)
ny=Image(x,y+1)-Image(x,y-1)
Это, как мы уже договорились, хранится
непосредственно в картинке. Т.е. для
каждой точки мы имеем 2-хбайтное значение.
С точки зрения ассемблера проще всего
достать его, используя POP HL.
difx=abs(vlx-nx)
dify=abs(vly-ny)
Подумаем... Использование функции модуля
здесь обусловлено тем, что дальше будет
вычисление корня, значения аргумента для
которого, как известно, должны быть
положительными. Но у нас корень
вычисляться не будет, вместо него мы
используем симметричную по обеим осям
таблицу (изображение круглого пятна).
Таким образом мы можем избавиться от
неудобной нам функции ABS():
difx=vlx-nx
dify=vly-ny
Но 2 вычитания - тоже не ахти как быстро.
Можно ли что-нибудь с этим сделать? Да,
можно! Вспомните что изображение пятна
света - круглое, т.е. симметрично по обеим
осям! А это значит, что неудобное нам
вычитание мы можем заменить на гораздо
более приятное сложение.
И еще одно: если ввести небольшое
дополнительное условие, то можно одним
выстрелом убить двух зайцев. :) Вспомните,
если мы будем доставать значения nx и ny
через POP HL, то соответственно у нас
будет H=ny и L=nx. Так вот, если принять
что vlx и vly у нас будут помещаться в
байт (чего хватает за глаза даже не смотря
на то, что это числа со знаком) и vlx+nx
не будут вызывать переполнения - то тогда
мы можем, разместив B=vly и C=vlx
реализовать оба сложения одной командой
ADD HL,BC!
Замечательно, правда? :)
Остались мелочи:
col=15-sqrt(sqr(difx)+sqr(dify))
if col>15 then col=0
Все это у нас уже учтено при построении
изображения светового пятна, так что можно
просто достать оттуда готовый байт.
plot x,y
... И упихать его на экран :)
Все!
Посмотрим, что же у нас получилось:
;SP = указатель в изображении
;DE = указатель на экране
;B = vly
;C = vlx
POP HL ;Достали nx и ny. H=ny, L=nx
ADD HL,BC ;Складываем сразу H=vly+ny и
;L=vlx+nx
LD A,(HL) ;Берем значение освещенности
;для данной точки. Как это
;получается - см. ниже.
LD (DE),A ;Пихаем байт на экран.
INC E ;Переходим к следующему байту
;на экране.
INC C ;Смещаем vlx для рассчета
;следующего байта.
Итого получаем 10+11+7+7+4+4=43 такта на
байт. Совсем неплохо... :)
Теперь о том, как же так получается, что
мы сразу берем значение освещенности из
таблицы после вычисления difx и dify. А
все просто - изначально к vly прибавляется
старший байт адреса расположения в памяти
таблицы с изображением пятна света. А
строчки таблицы располагаются с адресов
кратных 256. Таким образом, мы каждый раз
после вычисления difx и dify (а проще
говоря - после ADD HL,BC) автоматически
получаем готовый указатель в таблице
освещенности.
Кстати, приведенный inner loop можно
ускорить еще на 6 тактов за счет
использования команды LDD:
POP HL
ADD HL,BC
LDD
Здесь мы автоматически получаем коррекцию
DE и BC. Правда, вместо INC C будет
выполняться DEC BC, поэтому появляются 2
отличия в построении таблиц:
- изображение должно располагаться в
памяти повернутым зеркально по X (так
чтобы при DEC C мы попадали на следующий
байт, а не на предыдущий).
- необходимо чтобы не происходило
переполнения (точнее перерасхода) значения
в регистре C, т.к. в это приведет к
изменению регистра B, что нежелательно. Но
это решается просто - изображение
светового пятна в таблице просто смещается
на некоторую константу и эта константа
плюсуется к начальному значению vlx
заносимому в регистр C. Однако при этом
нельзя забывать о том, что нельзя
допустить переполнения при вычислении
vlx+nx (в ADD HL,BC).
Таким образом все получается несколько
неудобно, зато inner loop будет работать
со скоростью 10+11+16=37 тактов/байт!
Да, хочу сразу предупредить, что этот
inner loop в 37 тактов я не опробовал, но
не вижу причин, почему он не должен
работать.
5. Вариации на тему bump mapping'а.
Первое что приходит в голову после
просмотра кучи реализаций bump mapping'а в
демах - "а почему они все такие
одинаковые"?
Начинает хотеться разнообразия. Об этом я
и хочу рассказать в данном разделе.
Самая главная вещь, которую хотелось бы
поменять - это форма пятна света. Ведь
куда ни посмотришь - везде круги :) А
хочется чего-то нового, интересного...
Почему, например, никто не сделает bump
mapping, у которого пятно света играет
лучами? Вот после таких мыслей я сел за
попытку реализовать bump mapping
принципиально отличающийся по виду и
возможностям. Результаты моей работы Вы
найдете в приложении к журналу, а здесь я
вкратце опишу основную идею.
Итак, нам надо заставить этот круг
двигаться. Для этого необходимо каждый
кадр формировать изображение пятна света.
Как же можно сделать пятно неправильной
формы? Очевидно, что в основе его лежат в
две вещи - формула окружности и таблица
синуса. Точнее некоторая циклическая
функция должна быть радиусом окружности в
каждой ее точке:
10 for i=0 to 2*pi step pi/32
20 let x=(f(i))*cos(2*pi/i)
30 let y=(f(i))*sin(2*pi/i)
40 plot x,y
50 next i
f(i) здесь - некоторая функция, задающая
радиус, например обычный синус. Важно
только чтобы функция была циклической и ее
период равнялся количеству итераций цикла.
Но считать это каждый кадр - дело
неблагодарное, да ведь еще надо
закрашивать эту неправильную фигуру
градиентом, расходящимся от центра к краям
и убывающим со скоростью пропорциональной
радиусу окружности в данной точке. Поэтому
поступим проще:
1) Создадим таблицу секторов окружности.
Нам необходимо знать для точки с
координатами (x,y) номер сектора
окружности, в который эта точка попадает.
Я не особо силен в математике, так что не
могу сказать, по какой формуле это все
считается :) Я пошел обходным путем и
просто нарисовал кучу расходящихся из
центра окружности линий, причем конец
каждой из них рассчитывался по формуле
окружности. Естественно все это
рисовалось не на экране, а в памяти и
линия ставила точки целым байтом. Взяв
потом центральную часть получившейся
картинки, я получил необходимую таблицу.
Но Вам это вряд ли придется делать, т.к.
в исходниках Вы найдете готовую таблицу.
2) Нам также потребуется таблица
градиентов. Она тоже лежит в готовом виде
в приложении.
Теперь для создания пятна света любой
формы все, что нам потребуется - нанести
градиент, соответствующий радиусу нашего
пятна в данной точке в точки принадлежащие
соответствующему сектору окружности. Как
это делается - лучше посмотреть
непосредственно в коде. Imho для любого
кодера это будет намного понятнее, чем
словесное объяснение :)
6. Исходные тексты
В приложении Вы найдете 2 набора исходных
текстов.
Первый из них иллюстрирует работу эффекта
в том виде, в котором он описан в
статье. Исходник взят из нашей демы Binary
Love т.к. это наиболее простой для
понимания код. Особо быстрым его не
назовешь, зато реализация практически
идентична описанному в статье алгоритму.
Исходник дан в формате TASM v3.0. Я
думаю, Вам не составит труда перенести его
в тот ассемблер, которым Вы пользуетесь.
Второй исходник иллюстрирует работу
эффекта описанного в предыдущем разделе. К
сожалению, в силу специфики моего кода,
он приведен в формате TASM v4.12 (c) RST7
и компилируется только в этом ассемблере!
Точнее, теоретически его можно перенести в
ALASM и ZX-ASM, но это потребует огромной
работы по переделке и подгонке исходника.
О переносе в STORM я просто умолчу - imho
легче написать все заново, чем перенести
мои исходники в этот ассемблер...
И что еще более печально для
пользователей ассемблеров отличных от TASM
v4.12 - подобные проблемы будут возникать
у Вас постоянно при попытках использования
моих исходников т.к. я настолько привык к
тем возможностям, которые предоставляет
TASM, что просто не могу писать код иначе.
Естественно, что если какой-то исходник
будет писаться специально для статьи - он
будет компилироваться везде, а вот если
это будет что-то из моих рабочих
исходников - Вам придется по любому
запускать TASM v4.12 чтобы откомпилировать
его.
7. Заключение
Надеюсь, что данная статья поможет вам
разобраться с принципами работы этого
эффекта. Вы можете спокойно использовать
приведенные в приложении исходные тексты
в своих программах, изучать их, подвергать
необходимым изменениям. Единственное что я
запрещаю делать со своими исходниками -
использовать их в Ваших программах без
упоминания моих копирайтов. Это относится
ко всем моим исходниками, которые уже были
опубликованы, а так же ко всем тем,
которые будут публиковаться в будущем.
Так же хочу обратиться ко всем кодерам на
Speccy. Если у вас есть что-то, о чем вы
хотели бы рассказать всем кодерам на
Спектруме - пишите, многим будет
интересно! Очень приветствуются статьи
подобные этой - с полным разбором
принципов действия какого-нибудь эффекта
или с описанием каких-то особых приемов,
позволяющих повысить быстродействие
какого-то эффекта.
Кроме того, интересно было бы узнать и
мнения тех, кому эти статьи адресованы -
что еще интересно спектрумовским кодерам
сегодня?
Одним словом - пишите, ваше мнение и
поддержка очень важны для нас!



