Из журнала Demo Or Die #1, 1999
__________________________________________
(C) by Wolf/eTC/Scene
Заливка треугольника.
Гуpо shading.
Наложение текстуры.
Исходя из того, что в компьютерной
3D-графике все 3D-объекты в основном
состоят из элементарных треугольников, в
данной статье будет описываться алгоритм
заливки одноцветного треугольника. Так как
на Спектруме в нормальном режиме (50fps),
в каждой точке не может быть свой цвет,
то мы рассмотрим треугольник залитый белым
цветом.
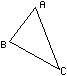
Возьмем любой треугольник с
точками ABC. Где A.X -
координата X точки A, а A.Y
- координата Y точки A
соответственно и т.д.
Заливать его будем
горизонтальными линиями,
т.к. этот метод является
самым быстрым и простым.
Прежде всего нам необходимо
отсортировать точки треугольника ABC по
координате Y по возрастанию. Минимальную
координату Y имеет точка A, максимальную
точка C, а среднее между ними значение
точка B.
Теперь зная что необходимо заливать
треугольник горизонтальными линиями от
точки A до точки C, необходимо визуально
построить этот треугольник по линиям (не
заливая его), но не рисуя его на экран, а
сохраняя в буфер координаты X всех трех
сторон образующих треугольник.
Т.е. мы будем иметь два массива
edge1[hgt_screen] и edge2[hgt_screen], где
hgt_screen - это высота экрана. В этих
массивах и будут располагаться координаты
X, которые и необходимо соединять
горизонтальными линиями между собой.
Для простоты и понимания, мы будем
строить визуально линию путем интерполяции
X координат. Для этого пусть у нас будет
процедура интерполяции
inter(x1,x2,len,buffer), где x1 - первая
координата (от куда), x2 - вторая
координата (куда), len - кол ичество
шагов, buffer - адрес буфера, куда
процедура будет помещать интерполированные
значения. Для тех кто не знает, то
интерполяция (в данном случае применяется
линейная интерполяция) - это отыскание
значений функций, соответствующим
промежуточным значениям аргумента,
которые отсутствуют в таблице (это нам так
в институте говорили). Ну а если объяснять
на "пальцах", то вот пример интерполяции:
X1 = 3
X2 = 9
len = 3
При таких начальных значениях,
интерполяционные значения будут следующими
3,6,9. Вот даже вам математическая
формула:
K=(1-step)*X1+step*X2
где K - промежуточное недостающее
значение, step - шаг, который должен
меняться в пределах [0...1], а X1 и X2 -
начальное и конечное значение
соответственно.
Вот пpимеp на асме:
;++++++++++++++++++++++++++++++++++++++;
; INTERPOLATIONS ;
; ;
; best idea: Wolf/eTc/ScEnE ;
; perfect code: Devil/eTc/sCeNE ;
; ;
; HL = BUFFER ;
; E = LEN OF BUFFER ;
; B = X1 ;
; A = X2 ;
;++++++++++++++++++++++++++++++++++++++;
INTER LD HX,B
CP B
LD C,A
LD D,A
LD A,#04
JR NC,INTER6
LD A,#05
LD D,B
LD B,C
INTER6
LD (INTER5),A
LD (INCDEC),A
LD A,D
SUB B
LD B,HX
CP E
JR C,INTER0
JR Z,INTER0
INTER3 LD C,A
DEC E
LD D,E
LD (HL),B
INTER4 SUB E
JR NC,INTER5
INC L
INC L
LD (HL),B
ADD A,C
DEC D
RET Z
INTER5 INC B
JR INTER4
RET
INTER0 INC A
LD C,A
LD D,E
LD A,E
INTER1 SUB C
JR NC,INTER2
ADD A,E
INCDEC INC B
INTER2 LD (HL),B
INC L
INC L
DEC D
JR NZ,INTER1
RET
Итак, построим визуально линии
треугольников (только координаты X) в
массивы:
{для понимания, на Паскале}
procedure visual_draw;
begin
inter(A.x,C.x,abs(A.y-C.y),edge1);
inter(A.x,B.x,abs(A.y-B.y),edge2);
inter(B.x,C.x,abs(B.y-C.y),edge2+
abs(A.y-B.y));
end;
{для тех кто не знает, функция abs() -
это модуль числа}
Проинтерполировав все эти координаты,
мы имеем два массива с координатами X-ов
всех трех сторон треугольника. Причем в
одном массиве одна сторона, а в другом две
остальные стороны.
Теперь нам ничего не остается делать,
как написать процедуру построения
горизонтальной линии. Назовем ее
Hline(x1,x2,y), где x1 и x2 -
горизонтальные координаты линии, а y -
собственно координата y этой линии.
И затем "залить" треугольник
горизонтальными линиями, следующим циклом:
y:=A.y;
for cycle:=1 to abs(C.y-A.y) do
begin
Hline(edge1[cycle],edge2[cycle],y);
inc(y);
end;
Вот и все, теперь если вы все поняли,
вы умеете заливать треугольники каким либо
цветом.
А теперь я расскажу алгоритм заливки
того же самого треугольника по Гуро. Гуро
- это линейная интерполяция освещенности
по изображению грани на экране.
Для этого нам необходимо создать еще
два массива color1[hgt_screen] и
color2[hgt_screen], которые будут хранить
интерполяционные значения освещенности. А
также назначить каждой точки треугольника
интенсивность освещенности (A.c, B.c, C.c,
где c - интенсивность освещенности).
Вот процедура заполнения граничных
массивов для треугольника по Гуро, она
такая же самая как и для заливки
треугольника произвольным цветом, но с
добавлением интерполяции освещенности:
procedure visual_draw_gouround;
begin
inter(A.x,C.x,abs(A.y-C.y),edge1);
inter(A.x,B.x,abs(A.y-B.y),edge2);
inter(B.x,C.x,abs(B.y-C.y),edge2+
abs(A.y-B.y));
inter(A.c,C.c,abs(A.y-C.y),color1);
inter(A.c,B.c,abs(A.y-B.y),color2);
inter(B.c,C.c,abs(B.y-C.y),color2+
abs(A.y-B.y));
end;
Имея процедуру построения
горизонтальной линии с линейной
интерполяцией цветов Hline_gouround(x1,x2,
c1,c2,y), где x1 и x2 - начальное и
конечное значение горизонтальной
координаты, а c1 и c2 - начальный и
конечный цвет, мы напишем процедуру
заливки треугольника по модели освещения
Гуро:
y:=A.y;
for cycle:=1 to abs(C.y-A.y) do
begin
Hline_gouround(edge1[cycle],
edge2[cycle],color1[cycle],
color2[cycle],y);
inc(y);
end;
С таким же успехом сюда же можно
"прицепить" и наложение текстуры, но при
этом необходимо каждой точке треугольнику
назначить координаты текстуры (u,v), где u
- координата X в текстуре, а v -
координата Y в текстуре. Ну еще и четыре
массива создать.
edge1u[hgt_screen];
edge1v[hgt_screen];
edge2u[hgt_screen];
edge2v[hgt_screen];
Тогда процедура визуализации для
текстурного треугольника будет выглядеть
следующим образом:
procedure visual_draw_texture;
begin
inter(A.x,C.x,abs(A.y-C.y),edge1);
inter(A.x,B.x,abs(A.y-B.y),edge2);
inter(B.x,C.x,abs(B.y-C.y),edge2+
abs(A.y-B.y));
inter(A.u,C.u,abs(A.y-C.y),edge1u);
inter(A.u,B.u,abs(A.y-B.y),edge2u);
inter(B.u,C.u,abs(B.y-C.y),edge2u+
abs(A.y-B.y));
inter(A.v,C.v,abs(A.y-C.y),edge1v);
inter(A.v,B.v,abs(A.y-B.y),edge2v);
inter(B.v,C.v,abs(B.y-C.y),edge2v+
abs(A.y-B.y));
end;
А теперь осталось только написать
процедуру заливки треугольника необходимой
текстурой, но для этого нам еще
понадобится процедура построения
горизонтальной линии со значениями цветов
из текстуры Hline_texture(x1,x2,
u1,v1,u2,v2,y), где x1 и x2 - начальное и
конечное значение горизонтальной
координаты, u1 и u2 - начальное и конечное
значение X в текстуре, v1 и v2 - начальное
и конечное значение Y и координата y,
которая указывает где выводить
горизонтальную линию на экране.
А вот и сама процедура заливки:
y:=A.y;
for cycle:=1 to abs(C.y-A.y) do
begin
Hline_texture(edge1[cycle],
edge2[cycle],edge1u[cycle],
edge2u[cycle], edge1v[cycle],
edge2v[cycle],y);
inc(y);
end;
Конечно в данной статьи я не описывал
методы оптимизации данных процедур(это
будет в следующем номере), но все таки
хотелось бы сказать пару слов.
Учитывая то, что на Спектруме - Гуро,
наложение текстуры и т.д. делается при
помощи "чанков" 4*4, можно заметить что
текстуры для "чанков" сильно "большими" не
бывают (т.к. "чанковкий" экран имеет
размер 64*48). Из этого следует, что лучше
всего располагать текстуру в памяти по
адресам кратным 256 (#c000,#c100,#c200
...). Я это делаю так:
org 25000
call init
...
start: halt
call action
...
jp start
org ($-1)/256*256+256
texture1 incbin "morda"
Это необходимо для того, что бы вы
интерполировали не просто координаты
текстуры, а сразу же их адреса. Старший
байт адреса будет соответствовать
координате Y, а младший байт координате X
текстуры. И тогда проинтерполировав
старшие и младшие адреса текстуры в
буфер, вы уже имеете абсолютные их адреса.
Вот вроде пока все на сегодня. Если я
как-то не правильно выразился или у вас
возникли вопросы, то пишите мне по таким
адресам: 2:4635/8.18 или scence#usa.net.
__________________________________________